1引言
鱼类经过数亿年的进化有了卓越的游动性能，人们对鱼类的形体结构和运动学展开了大量研究。在自然界中，约85%的鱼类以身体和(或)尾鳍(Bodyand/orCaudalFin，BCF)模式实现推进，这类推进模式具有速度快、能量传递效率高等优点，是最常见的机器鱼设计模式。BCF推进模式又可细分为不同的科类模式，如鳗鱼(鳗鲡科)就是以波动推进为主，这是一种几乎全身参与推进的方式。
近年来，越来越多的研究表明，在游动过程中，鱼类存在被动机制，其稳定游动所需的大部分力量由鱼体前部和中部的肌肉组织产生，鱼体后部的肌肉组织只负责将力量传递到尾巴。这为机器鱼的设计提供了思路，可通过适当地改变推进结构的刚度和鱼体的柔顺性，有效提高机器鱼的游动性能。如Fiazza等设计了具有顺应尾部的机器鱼，通过身体固有的频率振动，可实现柔顺尾部的摆动。White等利用仿生金枪鱼研究身体柔软性的作用，实验结果表明，增加身体的柔软性可以提高机器鱼推进的游动速度。Zhong等设计了一种由主动驱动的身体和柔顺的尾巴相结合的机器鱼，其能够实现高效游动，还设计出了这类机器鱼一般的运动学模型，并将该方法扩展到不同的游动模式中。这些研究在一定程度上说明，在一定条件下，被动机制(即顺从运动)可以提高机器鱼的游动性能。基于相关究，本文利用欠驱动和顺从运动的原理，提出用两段主动体结合两段被动顺从体来设计机器鳗鱼的方法。
深度强化学习(DeepReinforcementLearning，DRL)结合了深度学习在感知方面的强大理解能力，以及强化学习的决策能力，可实现端到端的学习。当DRL应用在机器人的控制问题上时，机器人由一个神经网络控制，不断与环境进行交互得到数据，并进行训练，可在不需要复杂模型和控制设计的情况下，直接解决机器人的控制问题。目前，已有许多将DRL应用在机器人控制方面的研究，如控制机械臂推动物体、控制两足机器人运动等，Li等也实现了软体机器人的运动控制。虽然学习延迟、样本实效等问题仍有待解决，但DRL在机器人控制上的一致性和泛化方面有很大的优势。机器鱼的运动控制现大多基于模拟鱼类运动学方程的方法，如Lighthill提出了行波方程。但这种近似的运动学方程并不能精确有效地描述所有鱼类的运动，此外，其是否最优的运动方式依有待验证。本文提出不设置运动学方程，利用DRL让机器鳗鱼在仿真环境中自主学习向前游动的能力，通过数据拟合得到机器鳗鱼的控制函数，从而实现对机器鳗鱼的控制，并通过相关实验验证了该方法的适用性。
2机器鳗鱼的设计
2.1基于主动体与被动顺从体推进机构的设计
Zhong等提出了一种新型的推进机构——主动体与被动顺从体推进机构(theActiveandCompliantPropulsionMechanism，ACPM)，用于构建机器鱼。其中，主动体部分采用拉线机构主动弯曲，被动部分是由弹性材料制成的柔性尾部。ACPM被证明具有鱼的波动运动特性，能够实现高速、高效地游动。
利用拉线机构可实现单电机对机器鱼多关节的控制，如图1所示。
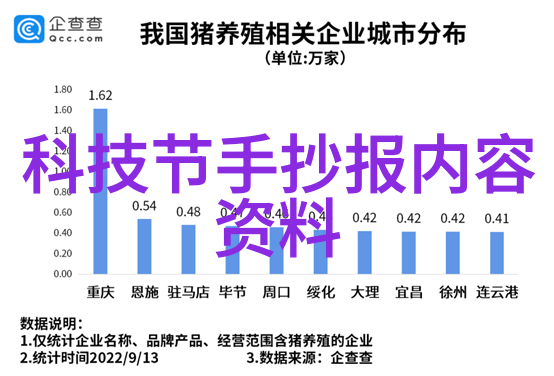
图1拉线机构的设计
在拉线机构中，舵机的旋转角
与鱼体的弯曲角
之间存在对应关系。假设各关节的摩擦力和旋转角度均相同，可得到
与
的映射关系：
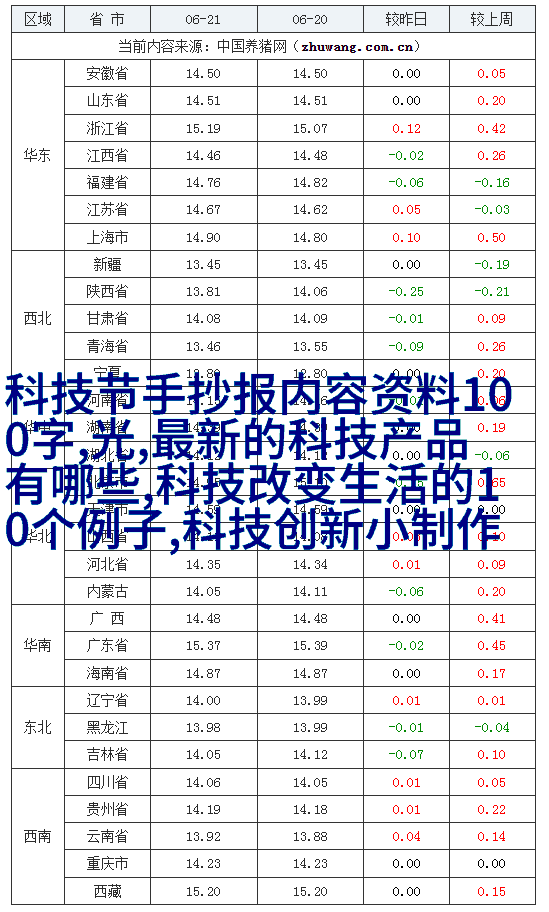(1)
其中，r为转盘的半径;N为关节数;d为两侧钢丝绳间的距离。
柔顺尾部的设计方法基于数学模型，详细的建模方法已经在本团队之前的工作中进行了介绍。在ACPM的后续研究中，Zhong等通过分析流体力矩和身体弯矩，将ACPM的建模方式拓展至其他游动模式中，如图2所示。图2展示了4种典型游动方式的力矩相位分布，红线La为流体力矩与身体转矩相互平衡的最佳身体长度。由图2可知，鳗鱼所属的鳗鲡科，存在两段被动顺从结构，而其余的模式只有一段顺从结构。基于该发现，本文采用两段主动拉线机构与两段被动柔顺身体相结合，来进行机器鳗鱼的设计，可使机器鳗鱼实现更高效地游动。如图3所示，当第一段拉线机构向一侧弯曲，第二段拉线机构向另一侧弯曲时，机器鳗鱼整体将呈现一个“S”型运动，这符合真实的鳗鱼游动方式。
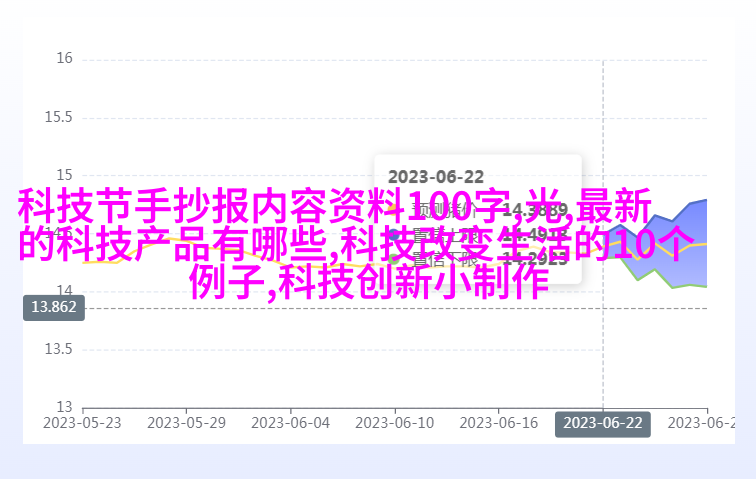
图2不同游动模式在ACPM中的优化
图3机器鳗鱼模型
2.2机器鳗鱼样机
本研究开发的机器鳗鱼由两段ACPM构成，由于不考虑下潜和上浮的功能，故不设计胸鳍。本文基于真实鳗鱼的形态，参考鳗鲡科在ACPM优化过程中的参数比例，结合实际需求，如电机的固定位置等，对机器鳗鱼进行设计。机器鳗鱼总长约550mm，横截面为椭圆，最大宽度为35mm，并逐渐减小。鱼身整体可分为6段，其中顺从身体长度为100mm，顺从尾巴长度为135mm。主动体部分采用拉线机构，利用直径为0.8mm的钢丝绳拉动，每一段拉线机构有4段间距相等的活动关节，4段活动关节的总长为80mm。顺从部分由硅胶浇铸设计好的模具制成，能够很好地满足被动柔顺的需求。头部和中间段身体为刚体部分，用于放置舵机和转盘，为防止钢丝绳被拉动时脱落，还设计了托臂。转盘、关节和刚体部分都通过3D打印技术制作而成，机器鳗鱼的实验样机如图4所示。
图4机器鳗鱼实验样机
两个舵机的型号均为Hitec的HS-5086WP，可提供3.6kg·cm的扭力。控制板选用ArduinoUNO，通过输出PWM信号来驱动舵机转动。控制板和电源等电子元件外置，通过杜邦线与舵机相连。由于顺从部分的质量较大，在两段拉线机构部分套上硅胶膜来增大浮力，并利用硅橡胶进行防水处理。此外，为限制机器鳗鱼的运动在同一水平面上，本研究还添加了铅块，用以调节样机所受到的重力和浮力。
3仿真优化的方法
3.1仿真环境
在深度强化学习过程中，借助神经网络，主体可直接从原始输入数据中提取和学习特征知识，并进行输出。因此，收集的原始数据的有效性格外重要。在机器人控制上，数据的收集一般有两种途径：第一种方式是在现实中直接收集数据，即将本研究的机器鳗鱼在水中连续测试并进行数据收集，但测试的工作量和难度较大，且本研究设计的柔性身体存在被动运动，机器鳗鱼在游动过程中，其位置和速度等数据变量将更为复杂，很难人工直接在数据库中进行特征提取;第二种方式是在仿真环境中获取数据，利用深度计算方法在感知方面强大的理解能力，有效地提取特征数据。就本研究而言，第二种方式有更好的适配性和训练速度。本文采用MuJoCo作为仿真平台，对机器鳗鱼做离散分割建模，并实现了有效控制。在仿真环境中进行深度计算，提高了鳗鱼模型参数的可调性，同时还赋予了深度计算过程更好的可视性，使参数变化对鳗鱼游动状态的影响更直观。
MuJoCo是一个通用物理引擎，能够快速准确地模拟关节类结构与其环境交互，已被广泛应用于基于模型的计算、数据分析、深度强化学习等相关领域的研究和实验。在MuJoCo中加入对应的水环境，将机器鳗鱼的运动限制在同一水平面上，以模拟浮力与重力的平衡，同时以室温20℃为标准，设置水环境的介质密度为1000kg/m3，介质黏度为0.001Pa·s，以模拟运动时机器鳗鱼受到的阻力和黏滞力。为减少仿真环境中的无用信息，本实验对仿真模型进行了一定程度的简化，如图5所示。机器鳗鱼整体长度保持为550mm，将两段放置舵机的分离刚体部件整合成一个整体作为刚体头部，以实现机器鳗鱼身体驱动的连贯性。除刚体头部外，驱动部分连成一体，由主动关节和柔性顺从体构成，不存在多余的刚体僵直，这种一体驱动的方式与真实的鳗鱼更接近。此外，本实验还简化了关节模型，并保留了两段ACPM中主动关节的耦合关系，这也是本文仿真控制的重点。为提高对柔性顺从体的仿真精度，本实验将两段顺从体分割成离散的分块，设置为被动关节，仅通过拉线机构的最后一段主动关节进行驱动，能够更好地模拟软体材料的柔顺特点。为提高模型的准确性，在实验中测试了顺从体的弯曲特性，并通过调整被动关节的特征参数，使仿真模型能够最大程度地接近真实鳗鱼。
图5MuJoCo中的机器鳗鱼模型
3.2深度强化学习
强化学习柔性动作-评价(SoftActor-Critic，SAC)算法是一个off-policy、actor-critic算法，与其他强化学习算法不同的是SAC将熵引入优化策略中，在获取更高累计奖励的同时，可将策略的熵最大化，熵越大，策略的随机性越大。策略熵允许高度随机的动作，在训练过程中，引入策略熵可丰富并拓展策略的探索过程，加速后续的学习并且防止策略过早地收敛至无意义的局部最优，鲁棒性较高。SAC算法的动作空间是连续的，不只是离散的阶段控制数据，因此，在解决连续控制问题上具有良好性能，适用于机器人的控制。
在利用深度强化学习进行训练之前，需要对机器鳗鱼的运动设置奖励函数、动作空间和状态空间。不同的奖励函数将导致不同的学习结果，若奖励函数不合适，可能导致最终结果不能收敛。本研究期望机器鳗鱼学习的运动能力是在静水中能够实现向前直线游动，且所需的输入转矩较小，即实现高效的直游。本文将训练机器鳗鱼的奖励函数R定义为：
(2)
其中，Vx为机器鳗鱼前进方向的速度;T为动作空间输入的转矩;Py为机器鳗鱼垂直于前进方向上的位置偏移;Posture_r为游动姿态，如头部的旋转角度;Safe_r为游动的安全性，用于排除机器鳗鱼游动过程中的异常姿态，如回旋前进等;
为转矩系数，表示转矩在奖励函数R中的参与权重;
为偏移系数，表示位置偏移在奖励函数R中的参与权重;
为姿态稳定系数，表示姿态在奖励函数R中的参与权重。
动作空间的设置必须与实际的控制输入数量相匹配。为了模拟拉线机构对活动关节的控制，每段拉线机构的4个关节应输入相同的值，以构成一个整体进行控制。本实验设置的输入信号范围为[-10,10]，当输入小于0时，活动关节向左旋转，当输入大于0时，活动关节向右旋转。
状态空间包括机器鳗鱼在仿真环境中所对应时刻的所有信息，包括多种力学特征，但在实际的控制中，获得的控制信息较少。本研究主要关注机器鳗鱼的运动姿态，因此，选择机器鳗鱼的位置和速度信息构成状态空间。
SAC算法需要对神经网络进行设置，本文的actor神经网络和critic神经网络的网络架构相同，均采用多层感知器神经网络，有2层隐藏层，每层有256个神经元，参数设置如表1所示。
表1深度强化学习参数表
将机器鳗鱼在仿真环境中训练200个周期，每个周期包括500步，每步的控制周期为10ms。为提高训练结果与真实水环境的适配性，在每个周期的第一步，本实验都设置一个随机影响值，模拟现实中位置和速度的偏差干扰。随机影响值越大，机器鳗鱼适应环境变化的能力越强，在训练过程中越难实现收敛;但随机影响值过小，则难以实现所期望的扰动效果。经过测试，本实验选用的随机影响值为0.01m，即为第一步的状态起始值加上[-0.01,0.01]m间的一个随机影响值。
通过调整奖励函数中
、
、
的值，可得到不同的训练结果，通过反复实验，能够得到较为适配的系数。通过实验发现，过小的转矩系数
对鳗鱼的控制影响较小，过大的
则会导致鳗鱼摆动的幅值减小;过小的偏移系数
对鳗鱼的偏移限制较小，过大的
则会出现鳗鱼模型摆动几次后依靠惯性滑行的现象。为保证神经网络的训练效果较为稳定，本实验最终将转矩系数
和偏移系数
的值分别固定为10-5和0.01，然后通过调整姿态稳定系数
的值，来训练不同性能的神经网络。
本实验将姿态稳定系数
的值依次设置为0.1、0.3、0.5、0.7，可得到4种不同的训练情况，如图6所示。通过判断总奖励值的变化程度，来近似表征训练过程的收敛性。首先计算总奖励值的滑动平均值，实现对总奖励曲线的滤波;然后计算平滑后总奖励曲线的斜率绝对值;最后将斜率绝对值持续小于0.5的曲线作为训练过程近似收敛的表征。当训练参数不同时，训练过程的近似收敛情况如表2所示。通过对比4种不同情况的训练结果可知，姿态稳定系数
的值越大，神经网络在训练过程中就越难收敛。
表2不同姿态稳定系数下的近似收敛步数
图6机器鳗鱼在不同的姿态稳定系数下的训练过程
在上述4种情况中，将得到控制效果稳定的神经网络在仿真环境中进行控制测试。每步的控制周期设置为10ms，在神经网络的控制下，让机器鳗鱼运行2000步，观察结果并收集数据。由于随机值的存在，机器鳗鱼在游动时的起始姿态是不同的，且游动步态需要经过一定的时间才能稳定，所以本实验选取第800步到第1200步之间的400步作为评估区间。
对于评估区间内4种不同姿态稳定系数，两段拉线机构的输出对比图如图7所示。其中，拉线机构的输出对应动作空间的输入，取值范围为[-10,10]。每隔4步，记录一次当前时刻两段拉线机构的输出，并计算平均值，共记录100组数据。实验结果表明，随着姿态稳定系数的增大，拉线机构的输出逐渐减小，且输出的幅值变化趋于稳定。此外，通过实验仿真发现，当拉线机构的输出过低时，机器鳗鱼的游动速度会明显降低。
由于本研究的目标是实现机器鳗鱼高效地直游，所以在机器鳗鱼游动过程中，必须关注其横向偏移值。因此，在评估区间内，本实验对4种姿态稳定系数下机器鳗鱼的偏移值进行了对比。让机器鳗鱼在每种姿态稳定系数下进行10次模拟，共得到40段评估区间，计算得到相同姿态稳定系数下的偏移值的平均值，如图8所示。当姿态稳定系数过低时，单次矫正的幅度过大，难以实现偏移量的减小;而当姿态稳定系数过高时，机器鳗鱼的单次矫正的幅度过小，同样难以实现偏移量的减小，即姿态稳定系数过低或过高都会导致游动偏移量过大，难以保证直游。此外，当姿态稳定系数过高时，偏移值的取值会更加分散，鲁棒性更低。
图8 四种不同姿态稳定系数下的游动偏移量
由图8可知，当姿态稳定系数
=0.3时，在输出和游动的稳定性上，经训练得到的神经网络性能较好，因此，选择该神经网络的输出对真实机器鳗鱼进行控制。
3.3控制函数
在姿态稳定系数
=0.3的神经网络中，本实验选择表现较好的一组输出进行控制拟合。对于评估区间内的两段拉线机构，将每个关节的转动角度按时间变化进行输出，发现关节转角的变化近似于三角函数，再通过算法进行曲线拟合，可以得到近似关节转角变化曲线，如图9所示。由图9可知，第一段拉线机构与第二段拉线机构的关节转角变化频率相同，频率为2Hz;第一段拉线机构的关节转动最大幅值为6°，第二段拉线机构的关节转动最大幅值为12°;且两者间存在相位差，为67°。由公式(1)可知舵机转角与关节转角的对应关系，进而得到舵机的控制函数，其中，r=16mm，N=4，d=22mm。
图9关节转角变化曲线
4实验结果
在实验平台上进行多次实验，以验证所得控制函数对机器鳗鱼样机的有效性。图10为本文设计的实验平台，其中，水池为180cm×140cm×60cm的长方体，摄像头安装在水池的上方，用来拍摄在水中游动的机器鳗鱼。
图10实验平台
4.1两段拉线机构驱动实验
本实验对机器鳗鱼两段拉线机构驱动的可行性进行测试。根据控制函数，设置两段拉线机构的频率为2Hz，关节转角幅值分别为6°和12°，相位差为67°。依次将机器鳗鱼设定为：(1)只有第一段拉线机构参与驱动;(2)只有第二段拉线机构参与驱动;(3)两段拉线机构都参与驱动。如图11所示，图中的绿线为起始线，以便对机器鳗鱼的游动表现进行对比。机器鳗鱼在0s时刻出发，当只有一段拉线机构驱动时，机器鳗鱼向前游动的速度较慢，并产生了横向偏移;当两段拉线机构协调驱动时，机器鳗鱼向前游动的表现良好。测试结果表明，两段拉线机构驱动能够有效驱动机器鳗鱼向前游动。
4.2游动速度实验
本文设计了速度测试实验，以直游速度为标准，将两段拉线机构的频率设置为2Hz，关节转角幅值分别保持为6°和12°，在不同相位差下，对机器鳗鱼的游动表现进行测量，以验证所得控制函数的有效性。由于所得控制函数的相位差为67°，所以本实验将相位差分别设置为40°、50°、60°、70°、80°、90°，固定控制函数的其他参数不变，进行对比实验。为排除游动不稳定对速度的影响，本实验设置了速度测试区，待机器鳗鱼稳定游入速度测试区后再进行速度计算。在每一种相位差下，都进行10次游动测试，通过计算得到平均速度，作为对照数据。表3为机器鳗鱼在不同相位差下的平均游动速度。由表3可图11机器鳗鱼在拉线机构驱动下的游动表现知，当相位差为67°时，机器鳗鱼的平均速度最大，这说明控制函数在直游中具有有效性。
表3机器鳗鱼在不同相位差下的游动速度
5讨论与分析
为拓展机器鳗鱼的摆动幅值极限，在仿真环境中，本实验将每个活动关节单侧的转角上限设置为35°，即每段拉线机构的最大摆动幅值是140°。但后续在对机器鳗鱼的训练过程中发现，第一段拉线机构的活动关节并不会达到最大转角，甚至整体的摆动幅值不会超过60°。对于机器鳗鱼的摆动频率，其取值在1.2~3.3Hz之间，这与现实中鳗鱼游动时的低频率、头部摆动的低幅相符合，说明该深度强化学习方法具有适用性。
对于鳗鱼类水下机器人，国内外常见的设计方式可分为以下几类：(1)采用多关节刚体设计，在每个关节放置驱动模块，通过电机等进行驱动，实现反复摆动，整体结构和控制一般都较为复杂;也有采用新型材料进行驱动，使用记忆合金和压电传感等新型材料实现鱼体的变形，从而实现推进，这类机器鳗鱼在能量转换方面存在弊端。(2)软体机器鳗鱼，通过磁感应、气泵等改变软体材料的局部特性，使其产生规律的变化，从而产生游动。与上述研究不同，本文的机器鳗鱼则利用鱼类游动的被动机制，采用刚性关节与柔顺身体连接的方式进行设计，包含这两者的特性，并在控制方面有更大的优势。
本文使用不基于给定运动曲线的方法，对鳗鱼直游控制进行研究，得到了近似正弦函数的控制结果，在一定程度上验证了正弦函数在仿生鱼直游控制中的合理性，也证明了本文方法的可行性。利用该方法可以对多种形态的水下仿生机器人进行游动学习得到优化的控制函数;同时，本文方法更适合复杂游动运动的控制，如逃逸、转弯等难以直接用运动学方程描述的运动，未来将会进一步探究复杂运动的学习优化。
6结论
本文利用鱼类游动的被动机制，设计了新型欠驱动机器鳗鱼，并建立了仿真模型，还利用DRL的方法让机器鳗鱼自主学习游动。在不同姿态稳定系数下，本文对神经网络的控制表现进行分析，并利用拟合函数在试验样机上进行控制测试，成功实现了直游。仿真和实验的结果证明了本文方法的有效性，这为类似结构的水下机器人的控制提供了思路。未来将对机器鳗鱼的模型进行优化，并改进控制拟合过程，进一步探究不同的身体参数以及其他运动参数对游动性能的影响。
